HESA Staff record 2012/13
Coding activities and cost centres
Version 1.0 Produced 2013-09-02
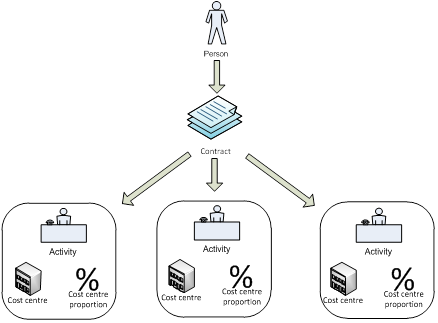
What are activities and cost centres?
Each contract must have at least one activity and an associated cost centre and a proportion: Activity.ACTSOC/Activity.CCENTRE/Activity.CCPROP. The activity associated with a contract defines the role of the staff member and the cost centre indicates where that activity takes place within the HEI. An individual contract may have up to three activities and associated cost centres returned. This could include a single activity in several cost centres, many activities in one cost centre, and so on.
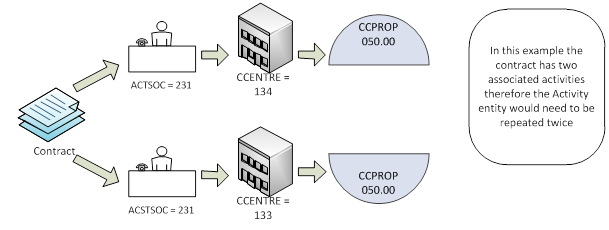
For example, an academic member of staff dividing their time equally between Cost centre 134 Catering and Hospitality Management and Cost centre 134 Business and Management Studies should be coded:
Why are activities and cost centres important?
There is an important tie-up between the Staff, Student and Finance Statistics records for Student: Staff Ratios and Unit Expenditure calculations amongst other uses. It is therefore useful to meet with colleagues who are responsible for the Student and Finance Statistics records in order to ensure consistency in reporting. A mismatch in the data returned for cost centres across the records could lead to your HEI appearing unusual in onwards use of the data.
Collection of cost centre data
The Institution profile record submitted by the HEIs in May-June of the reporting year collects information on the campuses and academic cost centres that will be used by the HEI in the Staff, Student and Finance Statistics records. HEIs are advised to agree their cost centres in advance of this return. Provision of data regarding the mappings of academic departments to cost centres is compulsory for HEIs in England, and optional for HEIs in Wales, Scotland and Northern Ireland. For the Institution profile record, assigning departments to academic cost centres is done on the basis of the full-time equivalence of academic staff, rather than that of student numbers. The FTE values reported in the Institution Profile record are forecasted and are not expected to match exactly the values reported in the Staff record.
The data collected in the Institution Profile return will be used to validate the Staff, Student and Finance Statistics returned. It is expected that in general, any academic cost centres which have staff FTE associated with them will also have student and finance data reported. Where there are mismatches between these records this will fail exception stage validation.
Allocating cost centres
Should the cost centre reflect the department which pays the salary?
Cost centres should be allocated against the source of funding for the contract as opposed to the actual activity undertaken. This ensures consistency between the Staff and Finance Statistics records, with a similar treatment being used in the Student record.
Can cost centres be split where a staff member works across several areas?
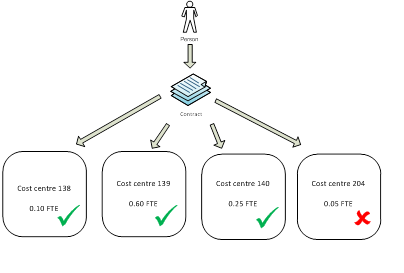
Yes, it is sometimes the case that as part of their contract staff resources will be split across multiple departments. Up to 3 cost centres and associated activities can be returned for each contract and the proportion of activity in each is captured in the Activity.CCPROP field. Where a member of staff is contracted to work in more than three cost centres as part of their role, the three cost centres where the most activity takes place should be returned.
For example:
A member of staff's contract activity is split across four cost centres. The HEI can only return three. The three in which the employee is most active are returned to HESA. The FTE would then need to be apportioned between the three remaining cost centres.
Proportion in cost centre
Activity.CCPROP records the proportion of the contract held in the cost centre. For example, if a member of staff spends 40% of their time in cost centre 134, Activity.CCPROP would be completed with 040.00.
Members of staff whose activity has moved from one cost centre to another within the reporting period should be reported within each relevant cost centre according to the time spent in each cost centre.
Note that the sum of all values in all occurrences of the Activity.CCPROP for a given contract's activities must fall within the range 099.7 - 100.3 in order to pass through validation.
Where a member only works for part of the year, should the proportion be reduced?
No, the proportion in the cost centre refers to the proportion of the contracted activity and not the proportion of the year therefore the sum of all occurrences of Activity.CCPROP should always equal between 099.7 - 100.3.
For example, a member of teaching staff whose contract runs from 01 August 2012 to 30 March 2013 and spreads their time evenly between Catering and Hospitality management, Business and Management Studies and Sports science & leisure studies would be coded as follows:
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>134</CCENTRE>
<CCPROP>033.3</CCPROP>
</Activity>
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>133</CCENTRE>
<CCPROP>033.3</CCPROP>
</Activity>
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>108</CCENTRE>
<CCPROP>033.3</CCPROP>
</Activity>
Coding Activity.CCPROP Examples
1. A member of staff's contract requires them to spend 30% of their time working in an academic capacity in the Art and Design cost centre, 40% of their time as an academic in the Media studies department and spends the remaining 30% of their working week as a warden in a student hall of residence.
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>143</CCENTRE>
<CCPROP>030.0</CCPROP>
</Activity>
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>145</CCENTRE>
<CCPROP>040.0</CCPROP>
</Activity>
<Activity>
<ACTSOC>614</ACTSOC>
<CCENTRE>204</CCENTRE>
<CCPROP>030.0</CCPROP>
</Activity>
2. A member of staff is contracted to spend 90% of their time in an academic capacity, spread evenly across three cost centres: Health and Community studies, Nursing and allied health professions and Pharmacy and Pharmacology. For the remaining 10% they work in a non-academic capacity in the Staff and Student Facilities cost centre.
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>105</CCENTRE>
<CCPROP>033.3</CCPROP>
</Activity>
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>103</CCENTRE>
<CCPROP>033.3</CCPROP>
</Activity>
<Activity>
<ACTSOC>231</ACTSOC>
<CCENTRE>107</CCENTRE>
<CCPROP>033.3</CCPROP>
</Activity>
In this example, although the staff member works across four different activities and cost centres, only three can be returned therefore only the main three are returned.
Contact Liaison by email or on +44 (0)1242 388 531.
